Note: this blog post is part of the F# advent calendar 2019.

Introduction

In this blog post, we’ll build a website that can solve Reverse Polish Notation (RPN) equations. All code (including the website) will be written in F#, but the equations themselves will be solved using WebAssembly.

Reverse Polish Notation

In RPN equations, operators (+, -, etc.) follow their operands (1, 3, etc.). This is known as postfix notation. Its main advantage: parentheses are no longer needed to define precedence. Consider the following equation (in standard mathematical notation):

(1 + 3) * (5 - 2)

This is the same equation, but specified in RPN:

1 3 + 5 2 - *

To solve this RPN equation we can just interpret its parts as a series of stack operations:

• Push 1 on the stack.
• Push 3 on the stack.
• Pop 3 from the stack. Pop 1 from the stack. Apply the + operator to the popped operands. Push 4 on the stack.
• Push 5 on the stack.
• Push 2 on the stack.
• Pop 2 from the stack. Pop 5 from the stack. Apply the - operator to the popped operands. Push 3 on the stack.
• Pop 3 from the stack. Pop 4 from the stack. Apply the * operator to the popped operands. Push 12 on the stack.

As you can imagine, the code to solve RPN equations will be a lot simpler than code to solve equations in standard mathematical notation, as the latter requires one to handle operator precedence rules and nesting (parentheses).

Side note: the famous Edsger Dijkstra invented the Shunting-yard algorithm to convert from infix notation to postfix notation.

In order for our website to be able to solve RPN equations, we’ll start by building a parser. As said, all our code will be written in F#.

Parsing

Each RPN equation is composed of:

1. Operands (the integers).
2. Operators (the functions).

We’ll model this as follows:

type Operator =
    | Add
    | Sub
    | Mul
    | Div

type Operand =
    | Integer of int

type Expression =
    | OperatorExpression of Operator
    | OperandExpression of Operand

type Equation =
    | Equation of Expression list

Our model allows for both empty- and invalid equations. A more advanced model would make illegal states unrepresentable, but for now we’ll keep it simple.

Not all equations will be valid though. There are three types of errors we’ll cover:

• Empty equations: no operands nor operators.
• Invalid equations: one or more unknown tokens.
• Unbalanced equations: equation does not resolve to a single operand.

We’ll model these errors as follows:

type EquationError =
    | Empty
    | Invalid of string
    | Unbalanced

Now on to the actual parsing. First, let’s try to parse an expression (which is either an operand or an operator):

let parseExpression (word: string): Result<Expression, EquationError> =
    match word with
    | "+" -> Ok(OperatorExpression Add)
    | "-" -> Ok(OperatorExpression Sub)
    | "*" -> Ok(OperatorExpression Mul)
    | "/" -> Ok(OperatorExpression Div)
    | Int32 i -> Ok(OperandExpression(Integer i))
    | _ -> Error(Invalid word)

This is fairly straightforward code, where we map strings to operator expressions and integers to operand expressions using a custom active pattern. Note that the return type is not an Expression, but a Result<Expression, EquationError>, as we also want to capture if the word we tried to parse was invalid.

Our next step is to convert a string to its words (represented as a list of strings):

module String =
    let words (str: string): string list =
        str.Trim().Split([| ' ' |], StringSplitOptions.RemoveEmptyEntries)
        |> List.ofArray

Using these two functions, we can start building the parse function:

let parse (str: string): Result<Equation, EquationError> =
    let words = String.words str
    let expressions = List.map parseExpression words
    ...

The expressions value has type Result<Expression, EquationError> list, so it is a list of Result’s. We’d like to convert it to a Result<Expression list, EquationError>, as we can then convert the Expression list to an Equation. We can flatten the Result list into a single Result using this function:

module Result =
    let ofList (results: Result<'a, 'b> list): Result<'a list, 'b> =
        let folder resultState resultElement =
            match resultState, resultElement with
            | Ok results, Ok element -> Ok(element :: results)
            | Error err, _ -> Error err
            | _, Error err -> Error err

        results
        |> List.fold folder (Ok [])
        |> Result.map List.rev

We are now able to create a complete, working version of our parse function:

let parse (str: string): Result<Equation, EquationError> =
    str
    |> String.words
    |> List.map parseExpression
    |> Result.ofList
    |> Result.map Equation

Let’s try calling our parse function to test it:

parse "1 2 +"
val it : Result<Equation,EquationError> =
  Ok
    (Equation
       [OperandExpression (Integer 1); OperandExpression (Integer 2);
        OperatorExpression Add])

Hurray! Parsing works. We’re not completely done with parsing though, as we have two types of errors that we haven’t checked for: empty- and unbalanced equations. To handle these cases, we’ll add the following function:

let validate (expressions: Expression list): Result<Expression list, EquationError> =
    let rec helper remainder stack =
        match remainder, stack with
        | [], [] -> Error Empty
        | [], [ OperandExpression _ ] -> Ok(expressions)
        | OperandExpression i :: xs, _ -> helper xs (OperandExpression i :: stack)
        | OperatorExpression i :: xs, OperandExpression _ :: OperandExpression _ :: ys ->
            helper xs (OperandExpression(Integer 0) :: ys)
        | _ -> Error Unbalanced

    helper expressions []

Using pattern matching and recursion, we’re walking through an Expression list and check to see if it is empty or unbalanced (an operator is found but not enough operands to work with). We can insert this function into our parsing pipeline using Result.bind:

let parse str =
    str
    |> String.words
    |> List.map parseExpression
    |> Result.ofList
    |> Result.bind validate
    |> Result.map Equation

Let’s verify that our pipeline detects these errors:

parse ""
val it : Result<Equation,EquationError> = Error Empty

parse "3 4 + -"
val it : Result<Equation,EquationError> = Error Unbalanced

Looks like it’s working!

REPL

Before we move on to the WebAssembly part, let’s build a tiny REPL in which we can solve RPN equations. First, let’s add code to evaluate (solve) an equation:

type EvaluationResult =
    | EvaluationResult of int

let evaluateExpression (stack: int list) (expression: Expression): int list =
    match expression, stack with
    | OperandExpression(Integer operand), _ -> operand :: stack
    | OperatorExpression Add, x :: y :: xs -> y + x :: xs
    | OperatorExpression Sub, x :: y :: xs -> y - x :: xs
    | OperatorExpression Mul, x :: y :: xs -> y * x :: xs
    | OperatorExpression Div, x :: y :: xs -> y / x :: xs
    | _, _ -> failwith "Invalid expression"

let evaluateEquation (Equation expressions): EvaluationResult =
    expressions
    |> List.fold evaluateExpression []
    |> List.head
    |> EvaluationResult

let evaluate (str: string): Result<EvaluationResult, EquationError> =
    parse str
    |> Result.map evaluateEquation

Here you can clearly see the stack-based algorithm reflected that we mentioned in the RPN introduction.

Now all that’s left is to create a REPL loop:

let printInstructions(): unit =
    printfn "Please enter an equation and evaluate it by pressing enter..."

let read(): unit =
    Console.ReadLine()

let eval (input: string): unit =
    evaluate input

let printOutcome (EvaluationResult outcome): unit =
    printfn "Outcome: %A" outcome

let parserErrorMessage (error: EquationError): string =
    match error with
    | Empty -> "Empty equation"
    | Invalid token -> sprintf "Invalid token: %s" token
    | Unbalanced -> "Equation is unbalanced"

let printError (error: EquationError): unit =
    let errorMessage = parserErrorMessage error
    printfn "Error: %s" errorMessage

let print (result: Result<EvaluationResult, EquationError>): unit =
    match result with
    | Ok outcome -> printOutcome outcome
    | Error error -> printError error

let loop(): unit =
    while true do
        read()
        |> eval
        |> print

[<EntryPoint>]
let main _ =
    printInstructions()
    loop()
    0

Simple and elegant. Let’s try out the REPL:

Please enter an equation and evaluate it by pressing enter...
1 2 +
Outcome: 3
2 4 * + 7
Error: Equation is unbalanced

Nice. We’re ready to move on solving RPN equations using WebAssembly.

WebAssembly

Before we dive into the details, let’s refresh our knowledge on what WebAssembly is. The official website has the following definition:

WebAssembly (abbreviated Wasm) is a binary instruction format for a stack-based virtual machine. Wasm is designed as a portable target for compilation of high-level languages like C/C++/Rust, enabling deployment on the web for client and server applications.

A great way to learn more about WebAssembly is to check out the cartoon intro to WebAssembly by Lin Clark. For now, just keep in mind that WebAssembly can be executed in the browser and that there is both a binary format (WASM) and a text format (WAT).

As said, our goal will be to have a website that can solve RPN equations. The first step is to parse the equation (using the code we just wrote). The parsed equation will then be compiled to (binary) WebAssembly code. The WebAssembly code is then executed in the browser. Finally, we’ll display the result of the solved equation as well as the WebAssembly used to solve it (binary and text format). Sounds fun? Let’s get to it!

Generating WebAssembly

In principle, we could be writing F# to output a generic RPN notation solver in WebAssembly, but to keep things simple, we’ll just compile the minimal WebAssembly needed to solve a RPN equation.

The stack-based algorithm used five types of operations:

• Push a number.
• Add two numbers.
• Subtract two numbers.
• Multiply two numbers.
• Divide two numbers.

If we look at the available WebAssembly instructions, we can find direct counterparts for all these operations, which we’ll model as follows:

type WebAssemblyInstruction =
    | I32Const of int
    | I32Add
    | I32Sub
    | I32Mul
    | I32Div

In our domain, we only support a single numeric type: 32-bit integers. In WebAssembly, these types are referred to as value types:

type WebAssemblyValueType = I32

For our purposes, a WebAssembly function can be modelled as a name, result type and a list of instructions:

type WebAssemblyFunction =
    { Name: string
      Result: WebAssemblyValueType
      Body: WebAssemblyInstruction list }

Functions in WebAssembly are always organized in a module. Our code will only ever have one function so we can make this a 1-1 mapping:

type WebAssemblyModule =
    { Function: WebAssemblyFunction }

We can now convert a parsed equation to its corresponding WebAssembly module:

let expressionToWebAssemblyInstruction (expression: Expression): WebAssemblyInstruction =
    match expression with
    | OperandExpression(Integer i) -> I32Const i
    | OperatorExpression Add -> I32Add
    | OperatorExpression Sub -> I32Sub
    | OperatorExpression Mul -> I32Mul
    | OperatorExpression Div -> I32Div

let equationToWebAssemblyCode (Equation expressions): WebAssemblyInstruction list =
    List.map expressionToWebAssemblyInstruction expressions

let equationToWebAssemblyModule (equation: Equation): WebAssemblyModule =
    { Function =
          { Name = "evaluate"
            Result = I32
            Body = equationToWebAssemblyCode equation } }

In a moment, we’ll write code to convert a WebAssemblyModule to WebAssembly text format (WAT) and binary format (WASM). Let’s start with defining some types for the WebAssembly output:

type WebAssemblyText = WebAssemblyText of string

type WebAssemblyBinary = WebAssemblyBinary of int list

type WebAssembly =
    { Text: WebAssemblyText
      Binary: WebAssemblyBinary }

We can now define the pipeline to compile a RPN equation to WebAssembly:

let equationToWebAssembly (equation: Equation): WebAssembly =
    let webAssemblyModule = equationToWebAssemblyModule equation

    { Text = Text.outputModule webAssemblyModule
      Binary = Binary.outputModule webAssemblyModule }

let convert (str: string): Result<WebAssembly, EquationError> =
    parse str
    |> Result.map equationToWebAssembly

This code will not compile, as we haven’t yet defined the functions to convert the module to text and binary format. Let’s fix this.

Text format

While the WebAssembly text format spec is great, Mozilla’s Understanding WebAssembly text format page was invaluable when trying to understand what the text format looks like in practice. In essence, a WebAssembly module is an s-expression, which is a recursive format designed to represent trees.

Here’s the WAT text we’d like to generate for the RPN equation: 1 2 +:

(module
  (func (export "evaluate") (result i32)
    i32.const 1
    i32.const 2
    i32.add))

There is not much to the WAT output we want to generate. It defines a module with one function. That function takes no parameters, has three instructions and returns an i32 value. Finally, the function is exported with the name “evaluate,” which will allow us to call it from JavaScript later.

The actual code to convert our WebAssembly module to its text format representation is fairly straightforward:

let outputValueType (valueType: WebAssemblyValueType): string =
    match valueType with
    | I32 -> "i32"

let outputResult (resultType: WebAssemblyValueType): string =
    sprintf "(result %s)" (outputValueType resultType)

let outputInstruction (instruction: WebAssemblyInstruction): string =
    match instruction with
    | I32Const i -> sprintf "i32.const %i" i
    | I32Add -> "i32.add"
    | I32Sub -> "i32.sub"
    | I32Mul -> "i32.mul"
    | I32Div -> "i32.div_32"

let outputBody (instructions: WebAssemblyInstruction list): string =
    instructions
    |> List.map outputInstruction
    |> String.concat " "

let outputExport (name: string): string =
    sprintf "(export \"%s\")" name

let outputFunction (function': WebAssemblyFunction): string =
    let export = outputExport function'.Name
    let result = outputResult function'.Result
    let body = outputBody function'.Body
    sprintf "(func %s %s %s)" export result body

let outputModule (module': WebAssemblyModule): WebAssemblyText =
    outputFunction module'.Function
    |> sprintf "(module %s)"
    |> WebAssemblyText

Tiny note: this code doesn’t output the code in an indented format, but it is semantically equivalent.

Binary format

The binary format is a bit more involved than the text format. Once again, the basis is formed by a module, which is represented as a list of bytes.

The first two parts of a module are fixed, and consist of a magic header and a version:

let outputMagicHeader: int list = [ 0x00; 0x61; 0x73; 0x6d ]

let outputVersion: int list = [ 0x01; 0x00; 0x00; 0x00 ]

Note that we defined the values in hexadecimal notation to have them correspond directly to how they are defined in the spec. We could have defined them as bytes, but for the sake of code brevity we’ll use regular ints.

Let’s move on to the contents of a module, which is comprised of zero or more sections. Each section consists of:

• A one-byte section ID.
• The u32 size of the contents, in bytes.
• The actual contents, which depends on the type of section.

While there are (currently) 12 different types of sections, we only need four of them:

type Section =
    | Type
    | Function
    | Export
    | Code

The first part of a section, its ID, can be output as follows:

let outputSectionIndex (section: Section): int =
    match section with
    | Type -> 0x01
    | Function -> 0x03
    | Export -> 0x07
    | Code -> 0x0a

The second and third part deal with the section’s contents. The second part is defined as the u32 size of the contents. If we examine the u32 spec, we can see that u32 values must be encoded using the LEB128 encoding. LEB128 encoding is a variable-length encoding, which means that different numbers can be encoded using a different number of bytes.

The LEB128 format has two different algorithms: one for unsigned integers and one for signed integers. Let’s start with the unsigned integers first:

let outputUnsignedLEB128 (i: int): int list =
    let bitEightMask = 0b1000_0000
    let bitsOneToSevenMask = 0b0111_1111

    let mutable more = true
    let mutable value = i
    let mutable bytes = ResizeArray<int>()

    while more do
        let mutable byte = value &&& bitsOneToSevenMask
        value <- value >>> 7
        more <- value <> 0

        if value <> 0 then byte <- byte ||| bitEightMask

        bytes.Add(byte)

    List.ofSeq bytes

Note that we used mutation here. While immutability is great, it is good to remember that not all F# code has to be immutable. Here, we only use mutation inside our function; it is an implementation detail. The actual returned value is a regular, immutable list.

The signed output is similar, but slightly different:

let outputSignedLEB128 (i: int): int list =
    let bitEightMask = 0b1000_0000
    let bitSevenMask = 0b0100_0000
    let bitsOneToSevenMask = 0b0111_1111

    let mutable more = true
    let mutable value = i
    let mutable bytes = ResizeArray<int>()

    while more do
        let mutable byte = value &&& bitsOneToSevenMask
        value <- value >>> 7

        if value = 0 && (byte &&& bitSevenMask) = 0 then more <- false
        elif value = -1 && (byte &&& bitSevenMask) > 0 then more <- false
        else byte <- byte ||| bitEightMask

        bytes.Add(byte)

    List.ofSeq bytes

Outputting an integer means choosing between the two LEB128 algorithms:

let outputInteger (i: int): int list =
    if i < 0 then outputSignedLEB128 i
    else outputUnsignedLEB128 i

As you might recall, the reason why we needed to output an integer was to output the length of the section’s code. In WebAssembly, bytes prefixed by their length are referred to as a vector:

let outputVector (bytes: int list): int list =
    let length =
        bytes
        |> List.length
        |> outputInteger
    length @ bytes

Outputting a section is then a simple combination of outputting its section index and its vector:

let outputSection (section: Section) (bytes: int list): int list =
    outputSectionIndex section @ outputVector bytes

Now that we have the basics defined, let’s move on to the output of the individual sections.

Type section

The type section encodes the function types of the functions defined in the module (of which we only have one). A function type is defined as the vector of a vector for the parameter types and a vector for the result (return) types:

let outputValueType (valueType: WebAssemblyValueType): int =
    match valueType with
    | I32 -> 0x7f

let outputResult (resultType: WebAssemblyValueType): int =
    outputValueType resultType

let outputFunctionTypes (function': WebAssemblyFunction): int list =
    let parametersCount = outputInteger 0x00
    let resultsCount = outputInteger 0x01
    let resultType = outputResult function'.Result
    let functionType = 0x60

    functionType :: parametersCount @ resultsCount @ [ resultType ]

let outputTypeSection (function': WebAssemblyFunction): int list =
    let functionCount = outputUnsignedLEB128 0x01
    let functionTypes = outputFunctionTypes function'

    functionCount @ functionTypes
    |> outputSection Section.Type

Function section

The function section links a function’s index to the function type. We have only one function, and thus only one function type, so we can hardcode the number of functions and the function index:

let outputFunctionSection: int list =
    let functionsCount = outputInteger 0x01
    let firstFunctionSignatureIndex = outputInteger 0x00

    functionsCount @ firstFunctionSignatureIndex |> outputSection Section.Function

Export section

In the export section, everything is listed that should be exposed to the “outside world.” When running WebAssembly in the browser, this means the exported values can be accessed from JavaScript. As we want to call our RPN solving function from JavaScript, we have to export our function.

As we only have one type we want to export (our function), we can use the following code:

type ExportType = FunctionExport

let outputExportType (exportType: ExportType): int =
    match exportType with
    | FunctionExport -> 0x00

Next, we’ll define a function to output a string, which we’ll use in a moment to define the exported function’s name:

let outputString (str: string): int list =
    str
    |> Seq.map int
    |> Seq.toList
    |> outputVector

Finally, we can glue these things together:

let outputExportSection (function': WebAssemblyFunction): int list =
    let exportsCount = outputInteger 0x01
    let exportName = outputString function'.Name
    let exportType = outputExportType FunctionExport
    let exportFunctionIndex = outputInteger 0x00

    exportsCount @ exportName @ [ exportType ] @ exportFunctionIndex |> outputSection Export

Code section

The final section is the code section, which contains (as you might have guessed) the code that a function will execute.

First, we’ll add a mapping from a WebAssembly instruction to its bytes:

let outputInstruction (instruction: WebAssemblyInstruction): int list =
    match instruction with
    | I32Const i -> 0x41: outputInteger i
    | I32Add -> [ 0x6a ]
    | I32Sub -> [ 0x6b ]
    | I32Mul -> [ 0x6c ]
    | I32Div -> [ 0x6e ]

Next, the body is defined as number of local declarations (of which we have none), the actual instructions, and finally a special marker for the end of the body:

let outputBody (instructions: WebAssemblyInstruction list): int list =
    let localDeclarationsCount = outputInteger 0x00
    let instructions = List.collect outputInstruction instructions
    let bodyEnd = 0x0b

    localDeclarationsCount @ instructions @ [ bodyEnd ] |> outputVector

The final code to output the code section is then simple:

let outputCodeSection (function': WebAssemblyFunction): int list =
    let functionCount = outputInteger 0x01
    let body = outputBody function'.Body

    functionCount @ body |> outputSection Code

Output module

Outputting a module is now a case of appending the outputs of the different sections:

let outputModule (module': WebAssemblyModule): WebAssemblyBinary =
    let typeSection = outputTypeSection module'.Function
    let functionSection = outputFunctionSection
    let exportSection = outputExportSection module'.Function
    let codeSection = outputCodeSection module'.Function

    outputMagicHeader @ outputVersion @ typeSection @ functionSection @ exportSection @ codeSection
    |> WebAssemblyBinary

And we’re done! We can now compiling any RPN equation to its WebAssembly format. Let’s start building the website now.

Building the website

To build the website using only F#, we can use the fabulous (pun intended) Fable compiler. Fable is a compiler that can compile F# code to JavaScript code. Precisely what we need!

Our website will use a particular flavor of Fable called Elmish. With Elmish, one can build applications using the Model-View-Update architecture that was popularized by Elm.

Our first step in building our Elmish application is to define the application’s model. In an Elmish application, the model is used as input to render the website. As such, the model should contain everything that we want to display on our website, which for our application looks like this:

type EvaluationResult =
    { Result: int
      Wasm: int list
      Wat: string }

type EvaluationError =
    | WebAssemblyException of exn
    | EmptyEquation
    | InvalidEquation of string
    | UnbalancedEquation

type Model =
    { Evaluation: Result<EvaluationResult, EvaluationError> option
      Equation: string }

The types are relative simple. There is an evaluation result that contains the result of the evaluation, as well as the generated WASM (binary format) and WAT (text format). The evaluation result itself is an optional part of the model (there is no evaluation initially). The other part of the model is the equation to solve.

For the first render of the website, Elmish requires us to provide a function that returns the initial model:

let init(): Model * Cmd<'a> =
    { Evaluation = None
      Equation = "" }, Cmd.none

Of course, we need to be able to update the model if we are to have any interactivity on our website. In the Elmish model, updating the model means sending a message. These messages are defined as a regular discriminated union:

type Msg =
    | UpdateEquation of string
    | EvaluateEquation
    | EquationEvaluatedSuccessfully of Evaluation
    | EquationEvaluatedWithError of EvaluationError

The next step is to define a function that takes a message and a model, and then returns a model and a command (we’ll get to what a command is):

let update (msg: Msg) (model: Model): Model * Cmd<'a> =
    match msg with
    | UpdateEquation newEquation ->
        { model with Equation = newEquation }, Cmd.none
    | EvaluateEquation ->
        evaluate model
    | EquationEvaluatedSuccessfully evaluation ->
        { model with Evaluation = Some(Ok evaluation) }, Cmd.none
    | EquationEvaluatedWithError error ->
        { model with Evaluation = Some(Error error) }, Cmd.none

The UpdateEquation, EquationEvaluatedSuccessfully and EquationEvaluatedWithError paths are relatively straightforward. They take a message with a payload and then update the model with that payload and return the model. These paths also return Cmd.none to indicate that there is no new message that needs to be processed.

The interesting path is the one where the user has requested that the equation be evaluated. The evaluate function calls the convert method, which takes an equation as input and returns the compiled WebAssembly:

let evaluate (model: Model): Model * Cmd<'a> =
    match convert model.Equation with
    | Ok webAssembly -> equationEvaluatedSuccessfully model webAssembly
    | Error error -> equationEvaluatedWithError model error

In the error case, we map the EquationError to an EvaluationError and then return the (unchanged) model and a new message indicating that the model should be updated with the error:

let equationEvaluatedWithError (model: Model) (error: EvaluationError): Model * Cmd<'a> =
    let evaluationError =
        match error with
        | Empty -> EmptyEquation
        | Invalid token -> InvalidEquation token
        | Unbalanced -> UnbalancedEquation

    model, Cmd.ofMsg (EquationEvaluatedWithError evaluationError)

This code shows that instead of just updating the model and returning Cmd.none, one could also choose to send a new command with a new message, deferring the actual updating of the model to the message handler.

For the success case, where an equation was successfully compiled to WebAssembly, we want to execute the WebAssembly in the browser. This means interacting with browser API’s. Many API’s have type-safe wrappers in Fable, but with the WebAssembly stuff being fairly new, we have to add those wrappers ourselves. Luckily, this is extremely easy:

[<AutoOpen>]
module WebAssembly =
    type Instance =
        { exports: obj }

    type ResultObject =
        { instance: Instance }

    [<Emit("WebAssembly.instantiate($0)")>]
    let instantiate (bufferSource: ArrayBuffer): JS.Promise<ResultObject> = jsNative

[<AutoOpen>]
module Uint8Array =
    [<Emit("Uint8Array.from($0)")>]
    let from (bytes: int list): ArrayBuffer = jsNative

As you can see, we define the browser API’s as regular functions, but with a special Emit attribute that Fable will use when converting the F# to JavaScript.

We now have all the infrastructure we need to execute our compiled WebAssembly:

let equationEvaluatedSuccessfully model webAssembly =
    let (WebAssemblyText(wat)) = webAssembly.Text
    let (WebAssemblyBinary(wasm)) = webAssembly.Binary

    let onSuccess webAssemblyInBrowser =
        EquationEvaluatedSuccessfully
            ({ Result = webAssemblyInBrowser.instance.exports?evaluate ()
               Wasm = wasm
               Wat = wat })

    let onError ex = EquationEvaluatedWithError(WebAssemblyException ex)

    let cmd = Cmd.OfPromise.either WebAssembly.instantiate (Uint8Array.from wasm) onSuccess onError
    model, cmd

Running our WebAssembly function is done through the interop code we just wrote: webAssemblyInBrowser.instance.exports?evaluate(). The evaluate() call is actually our compiled and exported WebAssembly function.

The last part of this function is instructing Fable to execute a function that returns a JavaScript promise (WebAssembly.instantiate), and call one of the two passed callbacks when the promise completed successfully or with an error.

The final step in building our website is to write functions to render our UI. With Elmish, rendering HTML is not done in a regular templating language, but using plain F# functions. Consider the following function to output the evaluation output contents:

let equationOutputContent (resultClass: string) (text: string): ReactElement =
    p []
        [ mark
            [ Name "result"
              Class resultClass ] [ str text ] ]

Calling equationOutputContent "tertiary" "3" will render the following HTML:

<p><mark name="result" class="tertiary">3</mark></p>

Did you note that the return type of the equationOutputContent function was of type ReactElement? This gives away the fact that Fable (by default) compiles to React code, in order to actually render the website.

In Elmish, rendering a UI is not much more than just composing functions. We’ll skip over the other functions, but if you’re interested in this bit you can just check out the source code.

And with that we now have a website where we can solve RPN equations using WebAssembly:

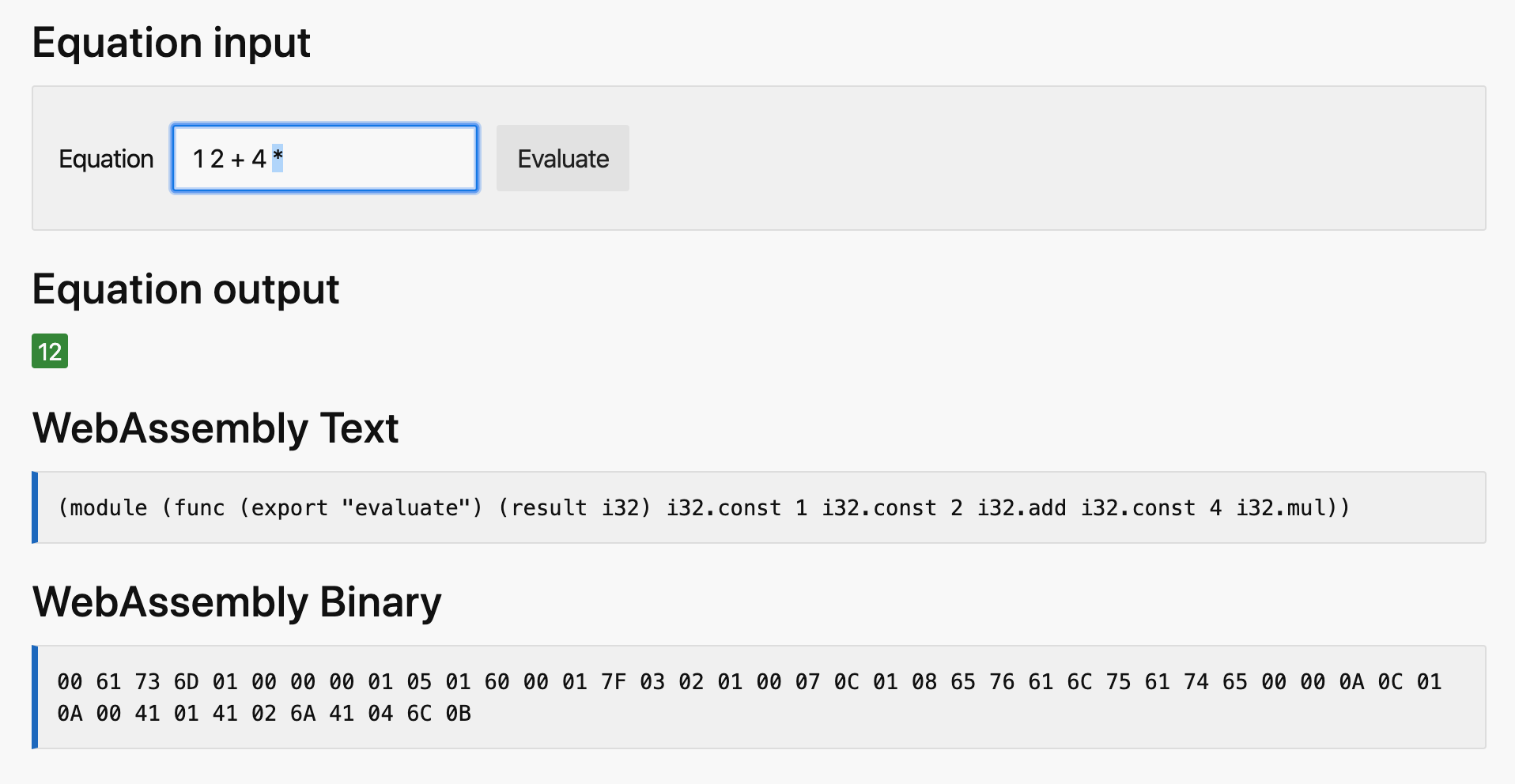
Conclusion

Using F# to parse and solve RPN equations was almost trivial. Modelling the domain using F#’s expressive and low-ceremony type system was an absolute joy. If you are interested in domain modeling using functional techniques, I highly recommend Scott Wlaschin’s Domain Modeling made Functional book.

Generating WebAssembly to solve RPN equations was not very hard. This was helped by the well-written WebAssembly specification. Building the website in F# using Fable was a first for me, but I absolutely loved it. The Elmish part especially was conceptually very appealing, with its simple, functional architecture. Defining HTML output using functions took some time to get used to, but when it did, I really liked it.

The source code of everything described in this blog post can be found at https://github.com/erikschierboom/krakow. You can try out the website at https://krakow-98706.firebaseapp.com/.